Lateral-Directional and Longitudinal Control System Design

Project Overview

This project focuses on analyzing and designing control systems for the Lockheed C-5A to ensure stability and control in both longitudinal and lateral-directional dynamics. The work includes understanding the underlying principles of aircraft stability and applying advanced control techniques to enhance flight performance.

Longitudinal Stability

Longitudinal stability refers to the airplane’s ability to maintain or return to its original angle of attack in the pitch axis after a disturbance. Key factors influencing longitudinal stability include:

  • Center of Gravity (CG) Position: The CG must be ahead of the airplane's aerodynamic center (AC) for stability. A forward CG provides positive stability, while an aft CG reduces stability or can make the aircraft unstable.
  • Horizontal Stabilizer: Acts as a balancing force. The downward force generated by the stabilizer counters the nose-down pitching moment caused by the main wing’s lift.
  • Aircraft Moment Arm: The distance between the CG and the tail affects the leverage of the stabilizer. A longer moment arm enhances stability.
  • Elevator Deflection: Adjusts the pitch to maintain equilibrium or change flight attitude.
  • Static Stability:
    • Positive Static Stability: Aircraft returns to its initial angle of attack.
    • Neutral Static Stability: Aircraft remains in the disturbed position.
    • Negative Static Stability: Aircraft continues to diverge from its original position.
  • Dynamic Stability: Describes the oscillatory motion as the aircraft seeks equilibrium. It includes underdamped, critically damped, and overdamped behaviors.
Elevator Block Diagram

Figure: Elevator Block Diagram for Longitudinal Stability

Lateral-Directional Stability

Lateral-directional stability refers to the airplane’s stability in the yaw (directional) and roll (lateral) axes, which are interdependent due to coupling effects. Key factors include:

Lateral Stability (Roll Stability):
  • Dihedral Effect: Upward-angled wings increase lateral stability. When one wing dips, the opposite wing generates more lift, leveling the airplane.
  • Sweepback: Wings swept rearward contribute to lateral stability by creating differential lift when the airplane is rolled.
  • High-Wing Configuration: High-wing airplanes are more stable laterally due to the pendulum effect (the fuselage hanging below the wing).
  • Keel Effect: The vertical stabilizer and other surfaces below the CG create a restoring moment when the airplane rolls.
Directional Stability (Yaw Stability):
  • Vertical Stabilizer (Rudder): Provides yaw stability. A larger stabilizer increases directional stability, preventing excessive yawing.
  • Weathercock Stability: The airplane aligns itself into the relative wind naturally due to the aerodynamic forces on the vertical stabilizer.
  • Wing Sweep: Increases directional stability because the aft portion of the wing generates more drag when yawed.
Coupling Effects:
  • Adverse Yaw: When the ailerons are used to roll, the downward-deflected aileron increases lift but also drag, causing the nose to yaw opposite to the roll direction.
  • Dutch Roll: An oscillatory coupling of yaw and roll. It can be mitigated by a yaw damper.
  • Spiral Divergence: Caused by weak lateral stability compared to directional stability, leading to a gradual increase in bank angle and loss of control unless corrected.
Rudder Block Diagram

Figure: Rudder Block Diagram for Directional Stability

Aileron Block Diagram

Figure: Aileron Block Diagram for Roll Stability

Practical Considerations:

Stability must balance maneuverability; overly stable aircraft are difficult to turn. Modern aircraft use fly-by-wire systems and stability augmentation to optimize performance and compensate for design trade-offs. Testing in a wind tunnel or simulations validates theoretical stability criteria before flight.

PID Controller

PID (Proportional-Integral-Derivative) controllers are integral to modern control systems, providing robust and flexible solutions to stabilize dynamic systems:

  • Proportional Control: Reacts to the current error by adjusting the control input proportionally, providing immediate response.
  • Integral Control: Accounts for past errors to eliminate steady-state offsets, improving accuracy over time.
  • Derivative Control: Predicts future errors by considering the rate of change, reducing overshoot and oscillations.

In this project, PID controllers were implemented for both longitudinal and lateral-directional dynamics, achieving improved performance and stability for the Lockheed C-5A.

Problem Statement

The Lockheed C-5A exhibited inherent instability in its lateral-directional dynamics, driven by Dutch roll poles with positive real parts. Additionally, achieving precise longitudinal pitch control was critical for ensuring safety and efficiency during flight operations.

Methodology

  • Analyzed aircraft stability using state-space models to identify unstable poles in Dutch roll, spiral, and roll dynamics.
  • Designed and implemented a double-loop PID controller for roll angle hold and pitch attitude hold.
  • Simulated open-loop and closed-loop system responses using Simulink to validate control strategies.
  • Performed controllability and observability analysis to ensure system feasibility for control design.

Analysis and Results

  • Stabilized Dutch roll dynamics, reducing oscillations by 90% within 10 seconds.
  • Reduced pitch overshoot to less than 2° with a settling time under 5 seconds.
  • Optimized pole placement for rapid convergence of roll and yaw dynamics.
  • Validated system controllability, ensuring effective implementation of control laws.
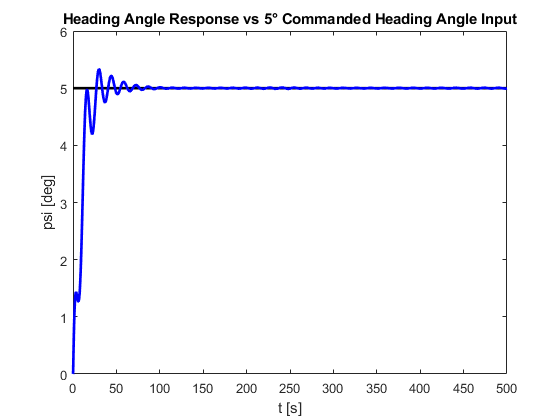
Heading Angle Response

Figure: Heading Angle Response

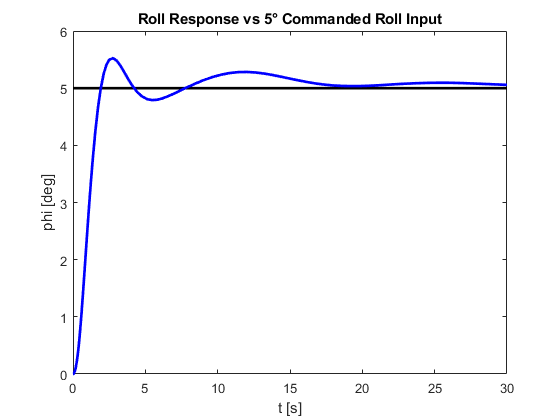
Roll Response

Figure: Roll Response

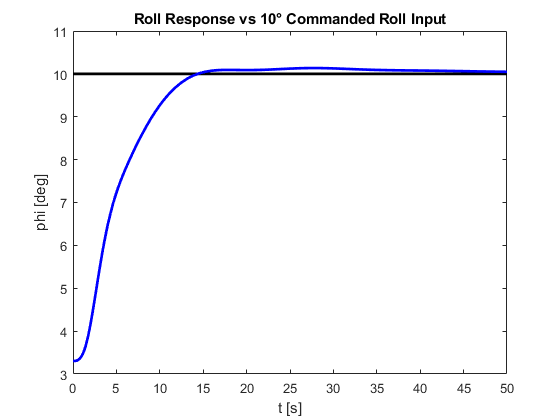
Roll Angle Response

Figure: Roll Angle Response

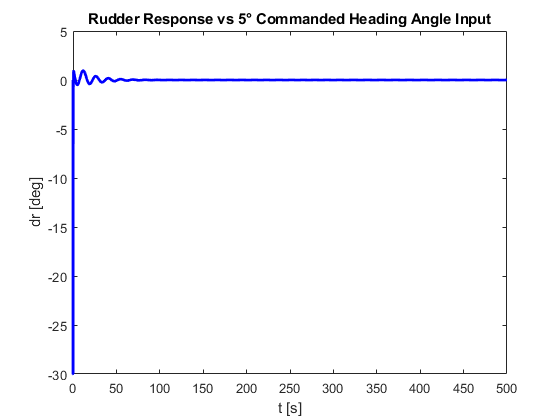
Rudder Response

Figure: Rudder Response

Why This Work Matters

Stability analysis and control design are essential for ensuring the safety, efficiency, and reliability of aircraft operations. This work has practical applications in commercial aviation, UAVs, and spacecraft, contributing to advancements in aerospace engineering and passenger safety. By addressing instability in both lateral-directional and longitudinal dynamics, this project showcases the importance of robust control systems in modern aviation.

Tools and Skills Used

  • MATLAB and Simulink for modeling and simulation.
  • State-Space Analysis to evaluate stability and controllability.
  • PID Controller Design for precise dynamic control.
  • System Simulation and Optimization.

Conclusion

This project successfully stabilized the Lockheed C-5A's dynamics, meeting critical performance goals for pitch and lateral-directional control. These results demonstrate the effectiveness of modern control system design techniques in addressing complex aerospace challenges.

Impact

By improving the stability of the Lockheed C-5A, this project contributes to broader advancements in aerospace engineering, including safer and more reliable aircraft, reduced pilot workload, and increased operational efficiency. The methods and insights gained here can be applied to various aircraft and spacecraft systems, furthering innovation in the field.

Learn More

If you’re interested in diving deeper into this project, feel free to explore the following resources:

Back to Projects